BIP est en retard

Du fait des frottements articulaires que nous ne savons pas encore bien compenser, nous sommes obligés de pousser les gains en position et vitesse pour espérer avoir un suivi de trajectoire potable, qui pour l'instant est encore à l'avenant. Bien loin des gains Kp/Kv choisis à 50/30 en simulation, nous avons dû monter à 1600/40 pour BIP Rhône-Alpes, et c'est encore loin d'être suffisant.

Le problème est que nous voyons apparaître des oscillations entretenues, une sorte de cycle limite qui peut être divergeant lorsqu'on pousse les gains (Seb, ce serait bien de récupérer un résultat de manip pour garder une trace écrite, genre avec exactement les mêmes gains que ceux que j'utilise en simulation juste après pour permettre une comparaison précise). C'est un comportement que nous retrouvons en simulation, figure suivante pour un échantillonnage de 10ms et des gains de 1400/37 qui provoquent d'ailleurs une divergence en milieu de simulation: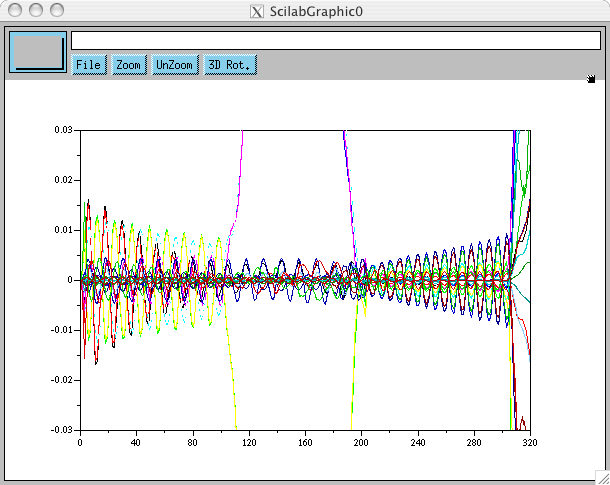

Or il se trouve que ces oscillations disparaissent complètement et la simulation est menée à terme sans difficultés lorsque l'on ne simule pas le retard de la loi de commande:

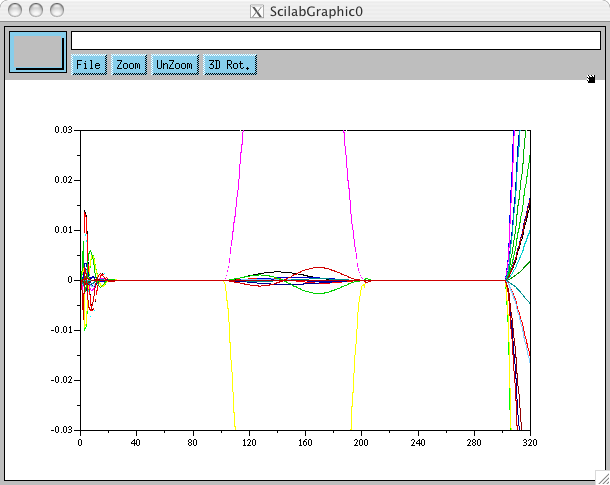Ces oscillations semblent donc être liées au retard (4ms écoulées sur le robot entre la mesure de l'état du système et l'application des couples correspondants, 10ms en simulation soit une simulation plus difficile qu'en réalité). Une solution presque naïve dans ce cas consiste à utiliser un prédicteur (de Smith dans le cas linéaire), c'est à dire tout bonnement de prédire l'état dans lequel sera le système 4ms ou 10ms plus tard, et à calculer la loi de commande pour cet état prédit, annihilant en théorie tout effet du retard. Puisque notre fonction de tâche est sensée linéariser la dynamique du système, à l'échantillonnage et au retard près (et aux erreurs de modèles près, mais ça n'est pas encore pris en compte en simulation), j'ai essayé un prédicteur des plus simples:

function [q_predite, qdot_predite] = predicteur(q, qdot, qddot, delta_t)
///////////////////////////////////////////
// Prediction de la position q_predite et de la vitesse qdot_predite du
// systeme un temps delta_t apres avoir ete dans la position q avec une
// vitesse qdot et une acceleration qddot.
///////////////////////////////////////////

  q_predite = q+delta_t*(qdot+delta_t/2*qddot);
  qdot_predite = qdot+delta_t*qddot;

endfunction

où q et qdot sont les valeurs observées sur le système et où qddot est issue du calcul de la loi de commande, une valeur toute théorique, donc. Le résultat est conforme à la théorie, c'est à dire que tout effet du retard disparaît, ni oscillation ni divergence:

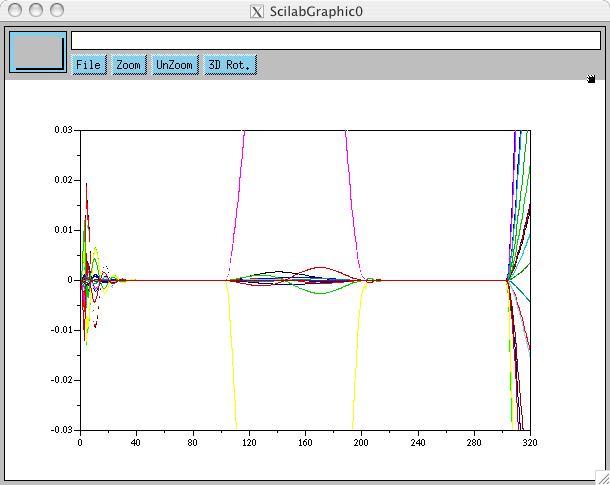Ce qui nous permet de monter les gains à 4300/77 où nous voyons réapparaître des oscillations de mauvaise augure, sans divergence toutefois:

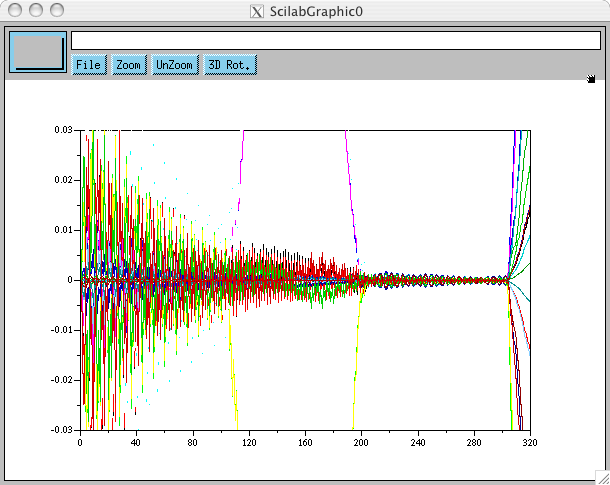On peut même monter à 4400/77, mais on peut estimer déjà là que les gains sont trop élevés. Si on utilise le même choix de gain dans une simulation sans retard, on ne voit pas ces oscillations:

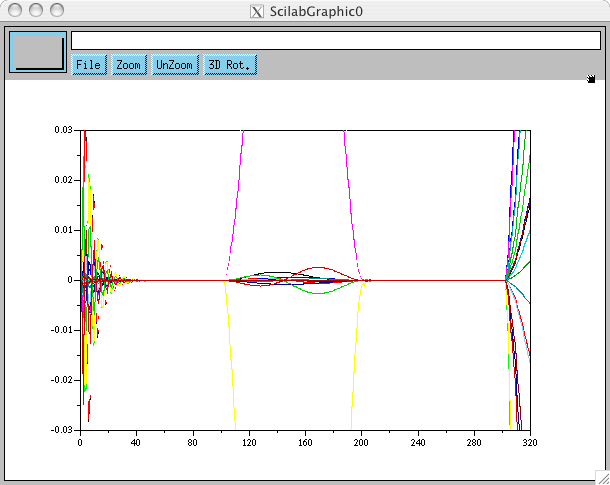On peut donc supposer qu'elles sont le résultat d'un prédicteur encore trop rustique (comme chacun sait, la dynamique du système n'est pas linéaire, évidemment), ceci-dit je vous propose de déjà commencer à l'utiliser sur le robot (on pourra voir ça à mon retour au labo lundi) sachant que le retard est bien moindre sur le robot que dans ces simulations. Pour info, voici la simulation (interrompue d'elle même) pour ce même choix de gain, 4300/77, mais sans ce prédicteur rustique:

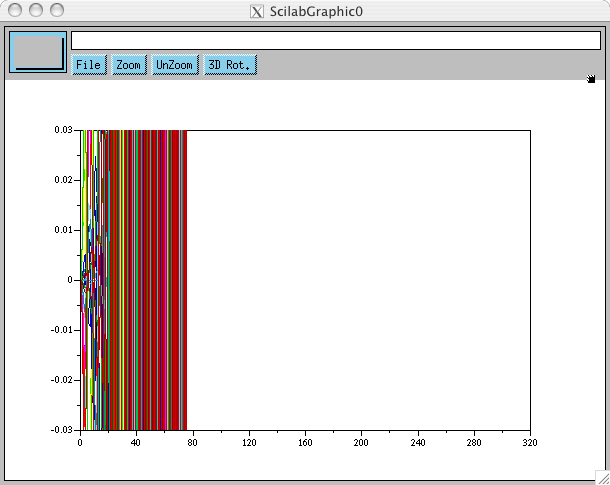Sans commentaire.

NB: tous ces tracés représentent la vitesse qdot du système.

-- PierreBriceWieber - 25 Mar 2004