You are here: SedWiki>Platforms/Misc Web>PlatformsObsolete>BipedeRobot>BipAnalyses>BipCalcPos (17 Jul 2007, SorayaArias)Edit Attach
Effet de l'approximation de CalcPos
Petite étude sur des résultats de simulation (donc à revoir ensuite sur des résultats de manip!) sur le calcul de qdot et qddot à partir d'un signal q donné et notamment sur l'impact potentiel du calcul de CalcPos qui n'est qu'approché, comme tout le monde sait. Tout d'abord, un signal q: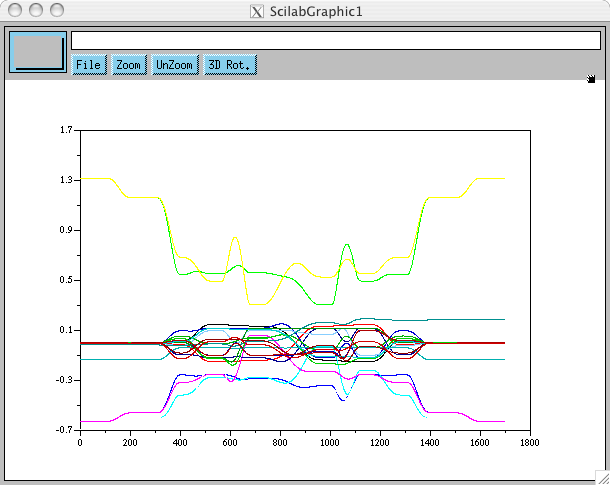 Soit nq=CalcPos(CalcMotors(q)), CalcMotors calcule les angles moteurs correspondants, c'est un calcul exact, CalcPos recalcule à partir de ces angles moteurs les positions articulaires, calcul inverse en théorie, mais calcul approché. nq - q vaut:
Soit nq=CalcPos(CalcMotors(q)), CalcMotors calcule les angles moteurs correspondants, c'est un calcul exact, CalcPos recalcule à partir de ces angles moteurs les positions articulaires, calcul inverse en théorie, mais calcul approché. nq - q vaut:
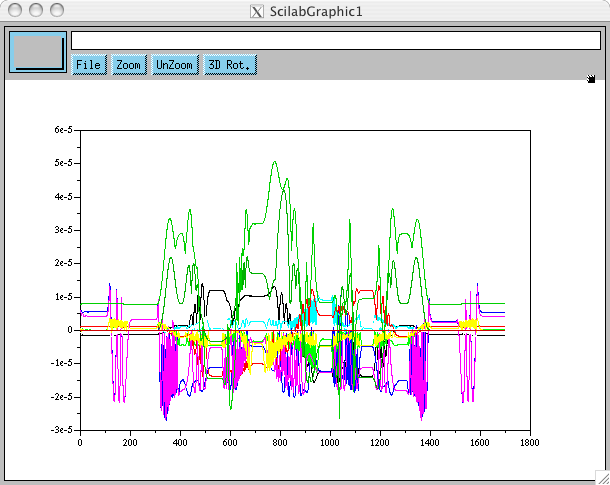 ce qui correspond à l'approximation que nous avons décidé de faire lors du travail de Jean-Jacques Parmentier, 1/200 degrés soit 8.7e-5 radians au maximum. Mais comme nous pouvons déjà l'observer, cette approximation a une dynamique, que nous n'avons encore jamais étudié.
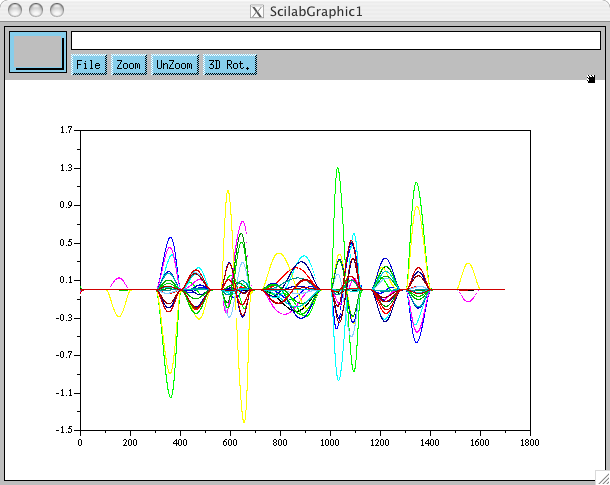
Soit maintenant %$\frac{q(t)-q(t-1)}{dt}$%, le calcul approché de qdot que l'on utilise dans la loi de commande du robot, on obtient un signal relativement propre pour cette simulation:
ce qui correspond à l'approximation que nous avons décidé de faire lors du travail de Jean-Jacques Parmentier, 1/200 degrés soit 8.7e-5 radians au maximum. Mais comme nous pouvons déjà l'observer, cette approximation a une dynamique, que nous n'avons encore jamais étudié.
Soit maintenant %$\frac{q(t)-q(t-1)}{dt}$%, le calcul approché de qdot que l'on utilise dans la loi de commande du robot, on obtient un signal relativement propre pour cette simulation:
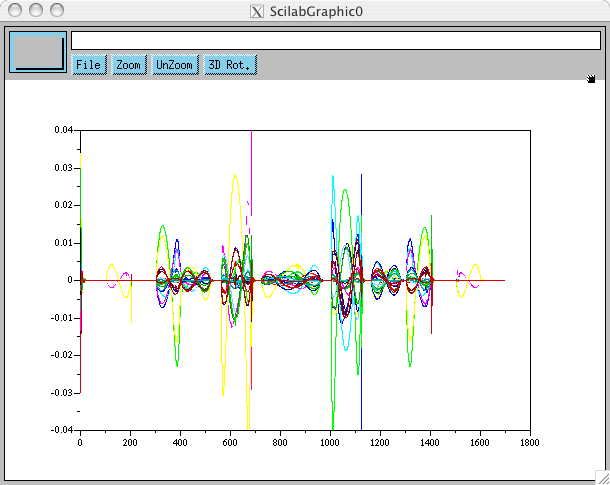
 Puisque la simulation nous fournit également qdot, on peut calculer l'erreur %$\frac{q(t)-q(t-1)}{dt} - q_{dot}$%:
Puisque la simulation nous fournit également qdot, on peut calculer l'erreur %$\frac{q(t)-q(t-1)}{dt} - q_{dot}$%:
 La théorie nous dit que le calcul %$\frac{q(t+1)-q(t-1)}{2dt}$% sera plus précis, et en effet, l'erreur %$\frac{q(t+1)-q(t-1)}{2dt} - q_{dot}$% vaut:
La théorie nous dit que le calcul %$\frac{q(t+1)-q(t-1)}{2dt}$% sera plus précis, et en effet, l'erreur %$\frac{q(t+1)-q(t-1)}{2dt} - q_{dot}$% vaut:
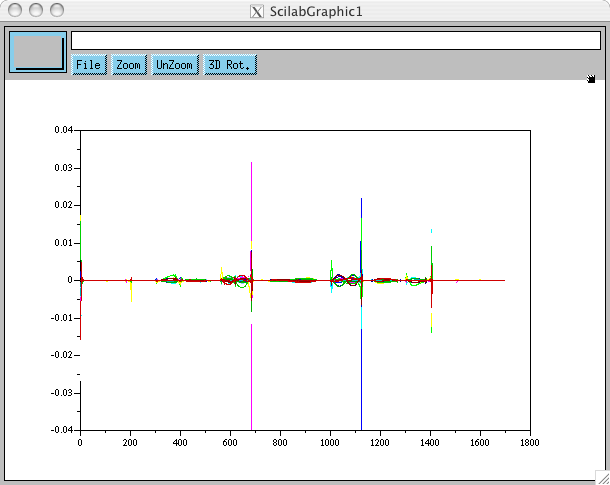 ce qui est beaucoup mieux sauf aux instants d'impact, mais ça on n'y peut rien. Si maintenant on refait le même calcul pour le signal passé par la moulinette CalcPos, l'erreur %$\frac{nq(t+1)-nq(t-1)}{2dt} - q_{dot}$% vaut:
ce qui est beaucoup mieux sauf aux instants d'impact, mais ça on n'y peut rien. Si maintenant on refait le même calcul pour le signal passé par la moulinette CalcPos, l'erreur %$\frac{nq(t+1)-nq(t-1)}{2dt} - q_{dot}$% vaut:
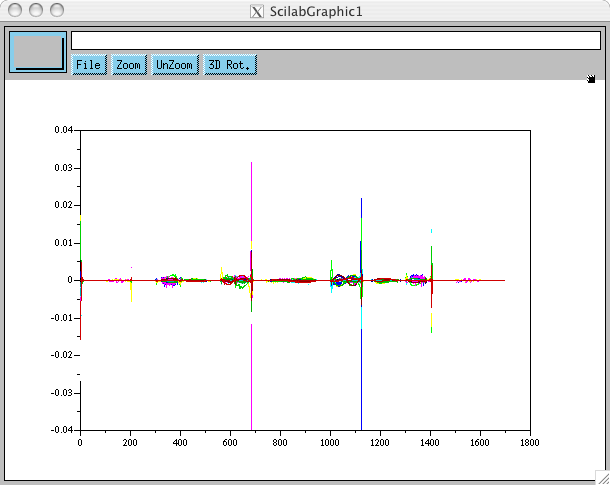 soit quelques zigouigoui supplémentaires. Un petit zoom nous donne dans le premier cas:
soit quelques zigouigoui supplémentaires. Un petit zoom nous donne dans le premier cas:
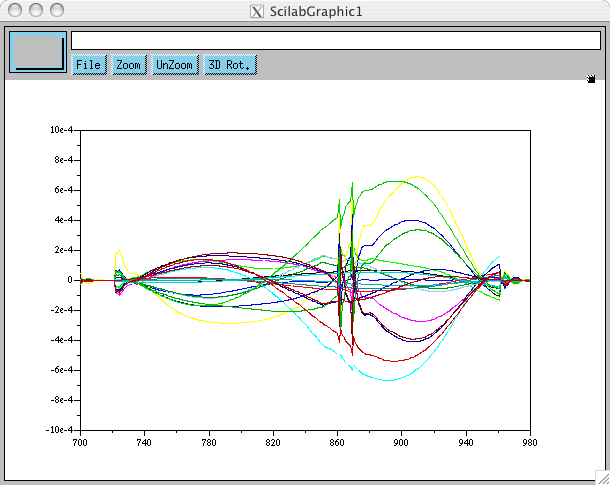 et dans le second:
et dans le second:
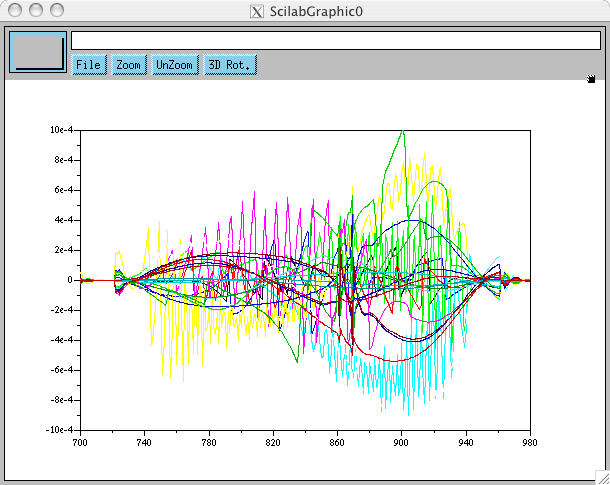 C'est manifeste, mais en même temps c'est d'une amplitude inférieure au pour-cent par rapport au signal d'origine, donc c'est peut-être pas très important: à surveiller.
Maintenant, pour pouvoir faire de l'identification, et en particulier l'identification des frottements sur laquelle nous nous penchons maintenant, on est également intéressés par l'accélération qddot. Connaissant q, qdot, les couples moteurs envoyés par la commande et l'état des contacts, on peut calculer la dynamique du système qui nous donne qddot:
C'est manifeste, mais en même temps c'est d'une amplitude inférieure au pour-cent par rapport au signal d'origine, donc c'est peut-être pas très important: à surveiller.
Maintenant, pour pouvoir faire de l'identification, et en particulier l'identification des frottements sur laquelle nous nous penchons maintenant, on est également intéressés par l'accélération qddot. Connaissant q, qdot, les couples moteurs envoyés par la commande et l'état des contacts, on peut calculer la dynamique du système qui nous donne qddot:
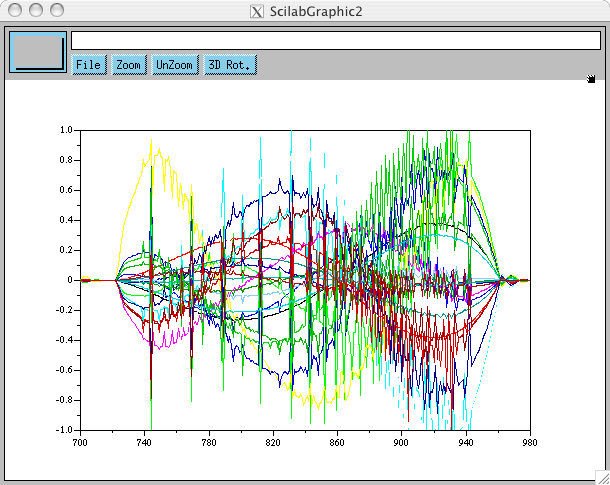 Le moins qu'on puisse dire est que ce nest pas propre. C'est pourtant exactement le calcul réalisé au cours de la simulation. Si maintenant on dérive numériquement le signal q, %$\frac{q(t+1)+q(t-1)-2q(t)}{dt^2}$% nous donne:
Le moins qu'on puisse dire est que ce nest pas propre. C'est pourtant exactement le calcul réalisé au cours de la simulation. Si maintenant on dérive numériquement le signal q, %$\frac{q(t+1)+q(t-1)-2q(t)}{dt^2}$% nous donne:
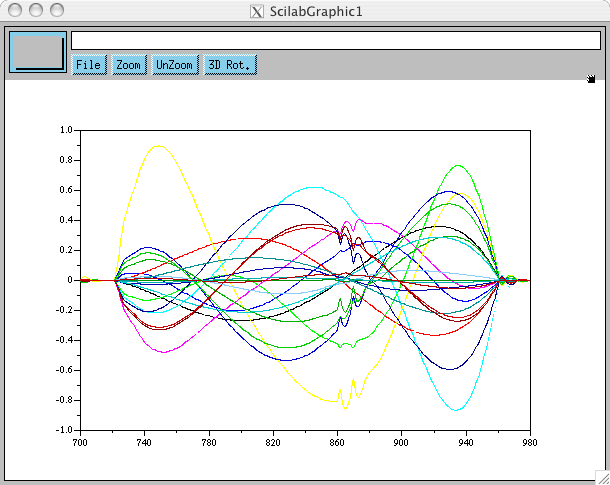 ce qui est sensiblement mieux, pour un calcul qui n'est pourtant qu'approché. La seule explication que je trouve, c'est que le premier calcul, exact, nous donne l'accélération instantanée alors que le second, approché, nous donne l'accélération moyenne sur 2 pas de temps, et au final le second calcul vaut mieux que le premier: c'est étonnant, mais c'est comme ça. Si maintenant on refait ce calcul pour le signal passé par la moulinette CalcPos, %$\frac{nq(t+1)+nq(t-1)-2nq(t)}{dt^2}$%, on retrouve le même type de zigouigoui:
ce qui est sensiblement mieux, pour un calcul qui n'est pourtant qu'approché. La seule explication que je trouve, c'est que le premier calcul, exact, nous donne l'accélération instantanée alors que le second, approché, nous donne l'accélération moyenne sur 2 pas de temps, et au final le second calcul vaut mieux que le premier: c'est étonnant, mais c'est comme ça. Si maintenant on refait ce calcul pour le signal passé par la moulinette CalcPos, %$\frac{nq(t+1)+nq(t-1)-2nq(t)}{dt^2}$%, on retrouve le même type de zigouigoui:
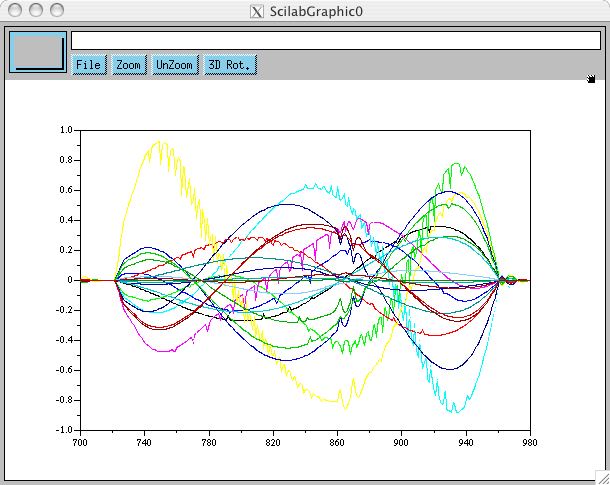 mais cette fois-ci plus tout à fait négligeables.
En premières conclusions, j'aurais donc tendance à dire que pour le calcul de qdot dans la loi de commande, on ne change rien mais on garde l'oeil ouvert, mais pour faire de l'identification, ce serait peut-être intéressant de sauvegarder le signal de position moteur avant qu'il ne passe par la moulinette CalcPos, qui introduit des artefacts. Maintenant, peut-être que tous ces résultats vont être bouleversés sur les résultats de manips: à voir.
-- PierreBriceWieber - 7 Apr 2004
mais cette fois-ci plus tout à fait négligeables.
En premières conclusions, j'aurais donc tendance à dire que pour le calcul de qdot dans la loi de commande, on ne change rien mais on garde l'oeil ouvert, mais pour faire de l'identification, ce serait peut-être intéressant de sauvegarder le signal de position moteur avant qu'il ne passe par la moulinette CalcPos, qui introduit des artefacts. Maintenant, peut-être que tous ces résultats vont être bouleversés sur les résultats de manips: à voir.
-- PierreBriceWieber - 7 Apr 2004 Edit | Attach | Print version | History: r4 < r3 < r2 < r1 | Backlinks | View wiki text | Edit wiki text | More topic actions
Topic revision: r4 - 17 Jul 2007, SorayaArias
 Copyright © by the contributing authors. All material on this collaboration platform is the property of the contributing authors.
Copyright © by the contributing authors. All material on this collaboration platform is the property of the contributing authors. Ideas, requests, problems regarding SedWiki? Send feedback
